TidalSim (Sampled RTL Simulation) Updates
Error Analysis
Caching and Parallelism API
Vighnesh Iyer
ATHLETE Small Update
Thursday, April 18th, 2024
Caching and Parallelism API
ATHLETE Small Update
Thursday, April 18th, 2024
Background
Sampled Simulation
Instead of running the entire program in uArch simulation, run the entire program in functional simulation and only run samples in uArch simulation
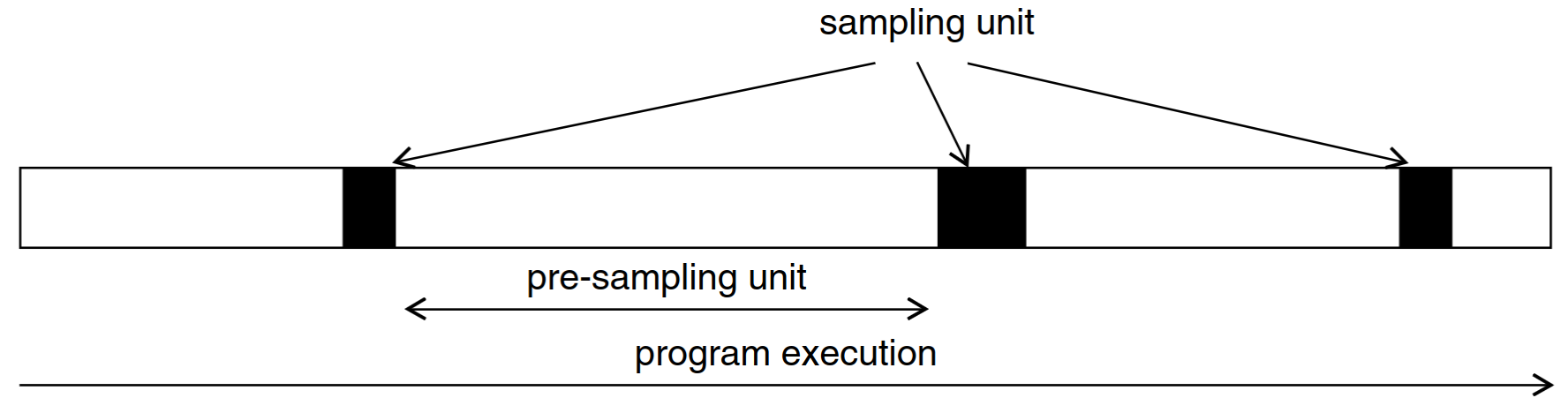
The full workload is represented by a selection of sampling units.
- How should sampling units be selected?
- How can we accurately estimate the performance of a sampling unit?
- How can we estimate errors when extrapolating from sampling units?
Existing Sampling Techniques
SimPoint

- Program execution traces aren’t random
- They execute the same code again-and-again
- Workload execution traces can be split into phases that exhibit similar μArch behavior
- SimPoint-style representative sampling
- Compute an embedding for each program interval (e.g. blocks of 100M instructions)
- Cluster interval embeddings using k-means
- Choose representative intervals from each cluster as sampling units
SMARTS

- Rigorous statistical sampling enables computation of confidence bounds
- Use random sampling on a full execution trace to derive a population sample
- Central limit theorem provides confidence bounds
- SMARTS-style random sampling
- Pick a large number of samples to take before program execution
- If the sample variance is too high after simulation, then collect more sampling units
- Use CLT to derive a confidence bound for the aggregate performance metric
Functional Warmup
The state from a sampling unit checkpoint is only architectural state. The microarchitectural state of the uArch simulator starts at the reset state!

- We need to seed long-lived uArch state at the beginning of each sampling unit
- This process is called functional warmup
Ideas Around Error Analysis
Sampled Simulation on wikisort
L1d functional warmup brings IPC error from 7% to 2%
Error Analysis
- Where does this 7% error come from? Why does it go down to 2%?
- For a given interval for which we know the IPC error, what parts contribute what amount to the error?
- How does the error breakdown change based on workload and sampling algorithm?
- How do we even break down the error? Can we leverage the access we have to full RTL simulation?
Sources of IPC Error
- Embedding error
- Error caused by representing one interval by a mix of sampled intervals
- Without sampling, there is no embedding error
- Functional warmup errors
- Error that wouldn't be present had the functional warmup of specific long-lived state was perfect (matched the full RTL simulation)
- Each additional long-lived block that's warmed-up has the effect of:
- Reducing error attributed to detailed warmup
- Adding (usually a smaller) error attributed to functional warmup
- Detailed warmup error
- Bias caused by starting IPC measurement for an interval only after detailed warmup is complete
- Error caused by difference of uArch state vs full RTL simulation (coupled to functional warmup)
- Time modeling error
- External model latent state errors
Error Analysis Methodology
- Simplifying assumptions
- Single-threaded workloads without time-related behaviors or I/O → No time modeling error
- External model latent state (DRAM MC model) contributes marginally to error → No latent state errors
- No sampling, every interval is simulated → No embedding errors
- Remaining error sources
- Functional warmup mismatches versus the golden RTL simulation + breakdown of per-block warmup errors
- Detailed warmup errors from interval offset measurement bias
- Error from the impact of functional warmup error on detailed warmup error
- How can we isolate each of these error sources?
Removing Embedding Errors
- If we only inject every interval's architectural state into RTL simulation, then we get a worst case per-interval error
- This error doesn't contain any offset measurement bias
- On its own, this error is the maximum error possible per interval
- Each extra thing we do (functional warmup, detailed warmup, warmup offset selection) serves to reduce this baseline error
- The remaining error can be attributed to deficiencies in functional or detailed warmup (marginal) + embedding error
Evaluating Detailed Warmup Errors
- We can first measure the impact of detailed warmup wrt the number of instructions and the offset (measurement bias)
- The error differences seen here are the errors mitigated by detailed warmup alone
Evaluating Functional Warmup Errors
- We can use a similar technique to measure the impact of functional warmup
- The final error model would also contain a term that describes the combined error reduction of functional and detailed warmup
Warmup Oracles
- 'Perfect' functional warmup with RTL simulation waveforms from the full run
- We can measure the impact of the warmup model vs the warmup oracle
- Detailed warmup is more tricky
- Emulating 'perfect' detailed warmup with our functional warmup model requires (likely impossible) state injection
Evaluation - Detailed Warmup Alone
For a given workload interval and a interval length $N$ (e.g. $N = 10000$) and without functional warmup, we can compute this table. (each cell is IPC error wrt the full RTL simulation)
| Detailed warmup instructions ($ n_{\text{warmup}} $) | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 100 | 500 | 1000 | 2000 | 5000 | ||
| Detailed warmup offset ($ n_{\text{offset}} $) | 0 | Worst case | Offset error ↑ Warmup error ↓ |
Offset error 2↑ Warmup error 2↓ |
Offset error 3↑ Warmup error 3↓ |
Offset error 4↑ Warmup error 4↓ |
Maximum offset error |
| -100 | Invalid | No offset error | '' | '' | '' | '' | |
| -500 | No offset error | '' | '' | '' | |||
| -1000 | No offset error | '' | '' | ||||
| -2000 | No offset error | '' | |||||
| -5000 | No offset error, best case | ||||||
Detailed Warmup Error Model
Given the data in the table for every interval and for different interval lengths $N$, fit the following model:
\[\begin{aligned}
\left(\frac{1}{\text{error}}\right) &= f(N, n_{\text{warmup}}, n_{\text{offset}}) \\
&= \frac{1}{1 + e^{-(n_{\text{warmup}}/N - \mu) / s}} + \alpha \frac{n_{\text{warmup}} - n_{\text{offset}}}{N} + \beta N
\end{aligned} \]
- Logistic term to model error reduction from warmup
- Linear term to model error reduction from offset elimination
- Linear term to model relationship of interval length to IPC error
- There might also be a term that mixes $n_{\text{warmup}}$ and $n_{\text{offset}}$ (TBD)
Extending the Error Model
- Consider building more tables with different functional warmup types (L1i, L1d, L2, BP, combinations) and fidelity (perfect vs model)
- Still an open question: how can we mix the functional warmup type/fidelity into the error model?
- Given a particular sampled simulation configuration ($N$, $n_{\text{warmup}}$, $n_{\text{offset}}$, functional warmup type + fidelity) for a given workload
- The remaining error from the table cell is attributable to inaccurate warmup (functional + detailed)
- Any additional error seen in actual sampled simulation is attributable to embedding
Caching and Execution Model
Complexity of the Flow
- We have a manual caching mechanism for every box input and output
- There is no exploitation of parallelism beyond RTL simulations
WIP: A Sampled Simulation Manager
- Basically a build system, dependency tracker, and parallel/distributed executor for sampled simulation
- Keys are dataclasses with
- Dependencies on other keys
- Outputs that can be files or in-memory Python objects
- Parameters that are used to determine whether a cache entry exists
- Rules (Python functions) for building the outputs from dependencies and parameters
- Simulation artifacts are placed on disk by the execution runtime
- Top-level flow requests keys and the key's rule operates on dependent keys (monadically, lazy)
- Build graph is constructed and execution is lazy