TidalSim: Fast, High-Fidelity, Low-Latency Microarchitectural Simulation
Functional Warmup, Error Analysis, Caching and Parallelism API
Vighnesh Iyer, Dhruv Vaish, Raghav Gupta, Young-Jin Park, Charles Hong, Sophia Shao, Bora Nikolic
ATHLETE Quarterly Update
Monday, April 29th, 2024
Motivation
- What are we trying to solve?
- Why is it worth solving?
Existing Hardware Simulation Techniques
| Examples | Throughput | Latency | Accuracy | Cost | |
|---|---|---|---|---|---|
| JIT-based Simulators / VMs | qemu, KVM, VMWare Fusion | 1-3 GIPS | <1 second | None | Minimal |
| Architectural Simulators | spike, dromajo | 10-100+ MIPS | <1 second | None | Minimal |
| General-purpose μArch Simulators | gem5, Sniper, ZSim, SST | 100 KIPS (gem5) - 100 MIPS (Sniper) | <1 minute | 10-50% IPC error | Minimal |
| Bespoke μArch Simulators | Industry performance models | ≈ 0.1-1 MIPS | <1 minute | Close | $1M+ |
| RTL Simulators | Verilator, VCS, Xcelium | 1-10 KIPS | 2-10 minutes | Cycle-exact | Minimal |
| FPGA-Based Emulators | Firesim | ≈ 10 MIPS | 2-6 hours | Cycle-exact | $10k+ |
| ASIC-Based Emulators | Palladium, Veloce | ≈ 0.5-10 MIPS | <1 hour | Cycle-exact | $10M+ |
- There is no simulation technique that meets all our criteria:
- High throughput: same order as interpreted ISA simulators
- Low latency: startup time ≈ RTL simulator compilation
- Accurate: small IPC errors, usable for evaluating optimizations
- Low cost: usable by academics
Accuracy of Microarchitectural Simulators
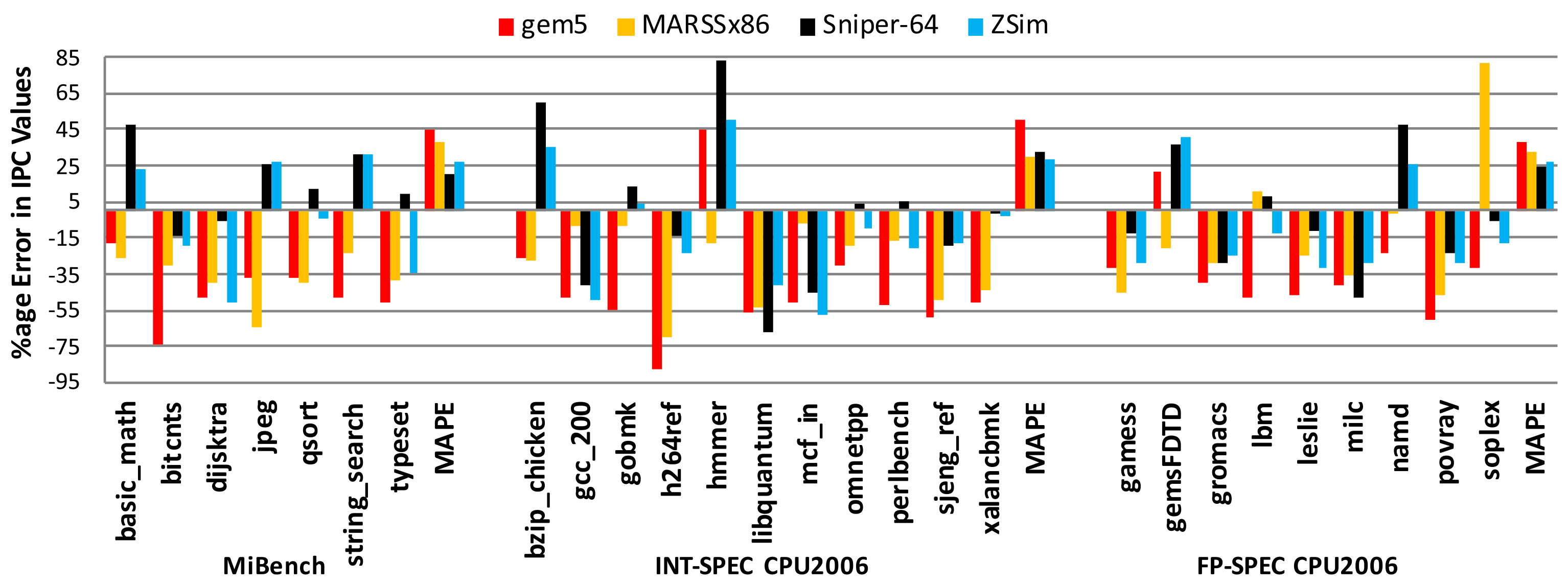
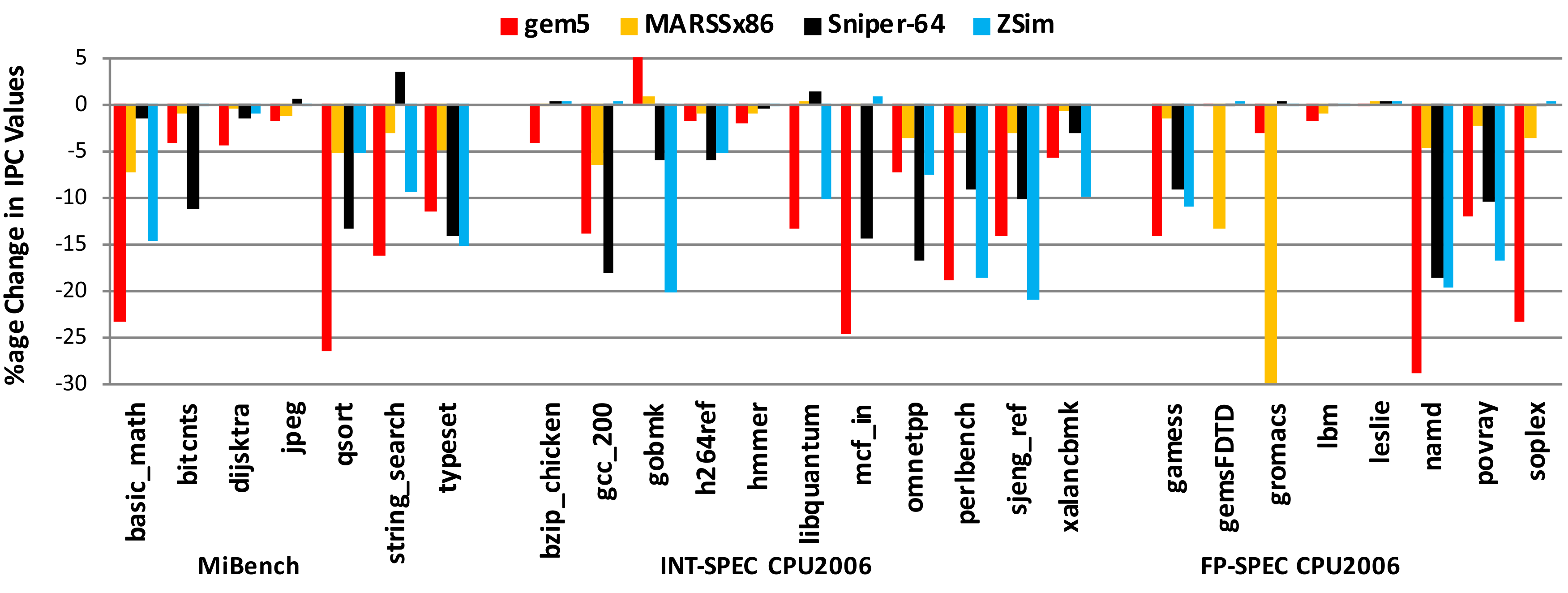
Trends aren't enough[2]. Note the sensitivity differences - gradients are critical!
uArch simulators are not accurate enough for microarchitectural evaluation.
[2]: Nowatzki, T., Menon, J., Ho, C.H. and Sankaralingam, K., 2015. Architectural simulators considered harmful. Micro.
What are we trying to solve?
We want a tool to evaluate microarchitectural changes on real workloads at high fidelity
The "Design-First" Methodology
- "Design-first", don't model!
- Build the whole system and evaluate it directly
- Iterate at the system-level
- Single source of truth
- Maintaining models that need to match the RTL creates more problems than it solves
- Iterate on the design directly
- This methodology works
- The "design-first" approach has built robust, high-performance open source RISC-V IP (rocket-chip, BOOM, Hwacha, Chipyard, Constellation) with small teams of grad students
- This methodology demands new tools
- FireSim: FPGA-accelerated deterministic RTL simulation
- But, FireSim isn't suitable for rapid iteration
Why Use RTL-Level Simulation?
- Eliminate modeling errors
- Remaining errors can be handled via statistical techniques
- No need to correlate performance model and RTL
- Let the RTL serve as the source of truth
- Can produce RTL-level collateral
- Leverage for applications in verification and power modeling
What are we trying to solve?
We want a tool to evaluate microarchitectural changes on real workloads at high fidelity
Why should we attempt RTL-level sampled simulation?
A critical tool that solves a long-standing problem to enable the "design-first" methodology
Background
Sampled Simulation
Instead of running the entire program in uArch simulation, run the entire program in functional simulation and only run samples in uArch simulation
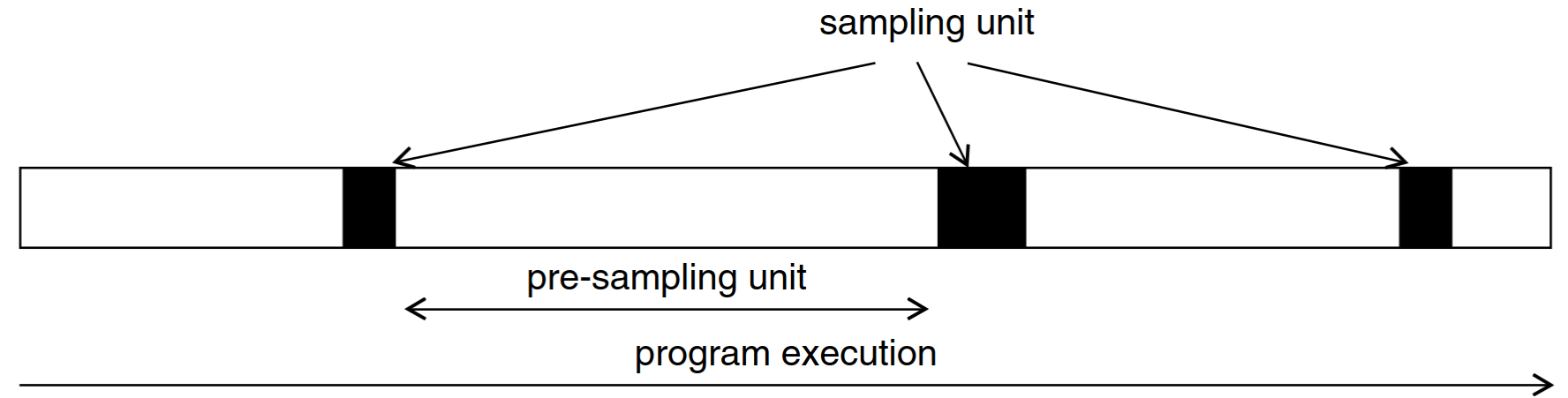
The full workload is represented by a selection of sampling units.
- How should sampling units be selected?
- How can we accurately estimate the performance of a sampling unit?
- How can we estimate errors when extrapolating from sampling units?
Existing Sampling Techniques
SimPoint

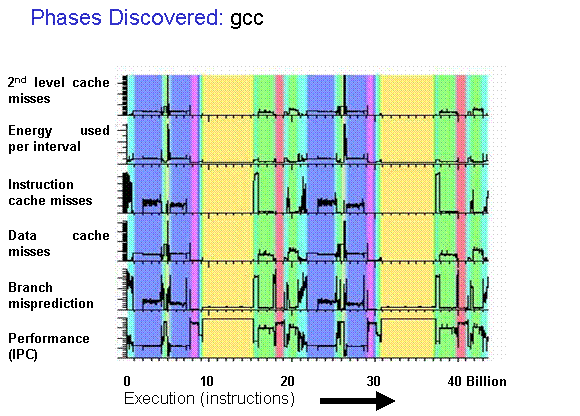
- Workloads can be split into phases that exhibit similar μArch behavior
- SimPoint-style representative sampling
- Compute an embedding for each program interval (e.g. blocks of 100M instructions)
- Cluster interval embeddings using k-means
- Choose representative intervals from each cluster as sampling units
SMARTS

- If we sample from a population, we can estimate the population mean
- SMARTS-style random sampling
- Pick a large number of samples to take before program execution
- If the sample variance is too high after simulation, then collect more sampling units
- Use CLT to derive a confidence bound for the aggregate performance metric
Functional Warmup
The state from a sampling unit checkpoint is only architectural state. The microarchitectural state of the uArch simulator starts at the reset state!

- We need to seed long-lived uArch state at the beginning of each sampling unit
- This process is called functional warmup
TidalSim Implementation
Overview of the TidalSim Flow
Implementation Details For TidalSim
- Basic block identification
- BB identification from spike commit log or from static ELF analysis
- Basic block embedding of intervals
- Clustering and checkpointing
- k-means, PCA-based n-clusters
- spike-based checkpoints
- RTL simulation and performance metric extraction
- Custom force-based RTL state injection, out-of-band IPC measurement
- Extrapolation
- Estimate IPC of each interval based on its embedding and distances to RTL-simulated intervals
Overall Functional Warmup Flow
- uarch-agnostic cache checkpoints as memory timestamp record (MTR) checkpoints
- MTR checkpoints → cache state with cache parameters and DRAM contents
- RTL simulation harness injects cache state into L1d tag+data arrays via 2d reg forcing
Memory Timestamp Record
- Construct MTR table from a memory trace, save MTR tables at checkpoint times
- Given a cache with n sets, group block addresses by set index
- Given a cache with k ways, pick the k most recently accessed addresses from each set
- Knowing every resident cache line, fetch the data from the DRAM dump
Results
Wikisort benchmark from embench, $N = 10000$, $C = 18$, $n_{\text{detailed}} = 2000$
L1d functional warmup brings IPC error from 7% to 2%
Results
Huffbench benchmark from embench, $N = 10000$, $C = 18$, $n_{\text{detailed}} = 2000$
Ideas Around Error Analysis
Sources of IPC Error
- Embedding error
- Error caused by representing one interval by a mix of sampled intervals
- Without sampling, there is no embedding error
- Functional warmup errors
- Error that wouldn't be present had the functional warmup of specific long-lived state was perfect (matched the full RTL simulation)
- Each additional long-lived block that's warmed-up has the effect of:
- Reducing error attributed to detailed warmup
- Adding (usually a smaller) error attributed to functional warmup
- Detailed warmup error
- Bias caused by starting IPC measurement for an interval only after detailed warmup is complete
- Error caused by difference of uArch state vs full RTL simulation (coupled to functional warmup)
- Time modeling error
- External model latent state errors
Error Analysis Methodology
- Simplifying assumptions
- Single-threaded workloads without time-related behaviors or I/O → No time modeling error
- External model latent state (DRAM MC model) contributes marginally to error → No latent state errors
- No sampling, every interval is simulated → No embedding errors
- Remaining error sources
- Functional warmup mismatches versus the golden RTL simulation + breakdown of per-block warmup errors
- Detailed warmup errors from interval offset measurement bias
- Error from the impact of functional warmup error on detailed warmup error
- How can we isolate each of these error sources?
Removing Embedding Errors
- If we only inject every interval's architectural state into RTL simulation, then we get a worst case per-interval error
- This error doesn't contain any offset measurement bias
- On its own, this error is the maximum error possible per interval
- Each extra thing we do (functional warmup, detailed warmup, warmup offset selection) serves to reduce this baseline error
- The remaining error can be attributed to deficiencies in functional or detailed warmup + embedding error
Evaluating Detailed Warmup Errors
- We can first measure the impact of detailed warmup wrt the number of instructions and the offset (measurement bias)
- The error differences seen here are the errors mitigated by detailed warmup alone
Evaluating Functional Warmup Errors
- We can use a similar technique to measure the impact of functional warmup
- The final error model would also contain a term that describes the combined error reduction of functional and detailed warmup
Backup Slides
Evaluation - Detailed Warmup Alone
For a given workload interval and a interval length $N$ (e.g. $N = 10000$) and without functional warmup, we can compute this table. (each cell is IPC error wrt the full RTL simulation)
| Detailed warmup instructions ($ n_{\text{warmup}} $) | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 100 | 500 | 1000 | 2000 | 5000 | ||
| Detailed warmup offset ($ n_{\text{offset}} $) | 0 | Worst case | Offset error ↑ Warmup error ↓ |
Offset error 2↑ Warmup error 2↓ |
Offset error 3↑ Warmup error 3↓ |
Offset error 4↑ Warmup error 4↓ |
Maximum offset error |
| -100 | Invalid | No offset error | '' | '' | '' | '' | |
| -500 | No offset error | '' | '' | '' | |||
| -1000 | No offset error | '' | '' | ||||
| -2000 | No offset error | '' | |||||
| -5000 | No offset error, best case | ||||||
Detailed Warmup Error Model
Given the data in the table for every interval and for different interval lengths $N$, fit the following model:
- Logistic term to model error reduction from warmup
- Linear term to model error reduction from offset elimination
- Linear term to model relationship of interval length to IPC error
- There might also be a term that mixes $n_{\text{warmup}}$ and $n_{\text{offset}}$ (TBD)
Extending the Error Model
- Consider building more tables with different functional warmup types (L1i, L1d, L2, BP, combinations) and fidelity (perfect vs model)
- Still an open question: how can we mix the functional warmup type/fidelity into the error model?
- Given a particular sampled simulation configuration ($N$, $n_{\text{warmup}}$, $n_{\text{offset}}$, functional warmup type + fidelity) for a given workload
- The remaining error from the table cell is attributable to inaccurate warmup (functional + detailed)
- Any additional error seen in actual sampled simulation is attributable to embedding
Caching and Execution Model
Complexity of the Flow
- We have a manual caching mechanism for every box input and output
- There is no exploitation of parallelism beyond RTL simulations
WIP: A Sampled Simulation Manager
- Basically a build system, dependency tracker, and parallel/distributed executor for sampled simulation
- Keys are dataclasses with
- Dependencies on other keys
- Outputs that can be files or in-memory Python objects
- Parameters that are used to determine whether a cache entry exists
- Rules (Python functions) for building the outputs from dependencies and parameters
- Simulation artifacts are placed on disk by the execution runtime
- Top-level flow requests keys and the key's rule operates on dependent keys (monadically, lazy)
- Build graph is constructed and execution is lazy
Conclusion
- We want to enable rapid RTL iteration with performance evaluation and generation of RTL-level collateral
- We need fast, low-startup-latency RTL-level simulation
- We propose TidalSim, a simulation methodology based on sampled RTL simulation
- Everything is open source
- TidalSim (github.com/euphoric-hardware/tidalsim) Forks of spike, chipyard, testchipip + top-level runner