TidalSim: Fast, High-Fidelity, Low-Latency Microarchitectural Simulation
Sampled RTL Simulation
Vighnesh Iyer, Dhruv Vaish, Raghav Gupta, Young-Jin Park, Charles Hong, Sophia Shao, Bora Nikolic
SLICE Summer Retreat
Monday, May 20th, 2024
Motivation
- What are we trying to solve?
- Why is it worth solving?
Existing Hardware Simulation Techniques
| Examples | Throughput | Latency | Accuracy | Cost | |
|---|---|---|---|---|---|
| JIT-based Simulators / VMs | qemu, KVM, VMWare Fusion | 1-3 GIPS | <1 second | None | Minimal |
| Architectural Simulators | spike, dromajo | 10-100+ MIPS | <1 second | None | Minimal |
| General-purpose μArch Simulators | gem5, Sniper, ZSim, SST | 100 KIPS (gem5) - 100 MIPS (Sniper) | <1 minute | 10-50% IPC error | Minimal |
| Bespoke μArch Simulators | Industry performance models | ≈ 0.1-1 MIPS | <1 minute | Close | $1M+ |
| RTL Simulators | Verilator, VCS, Xcelium | 1-10 KIPS | 2-10 minutes | Cycle-exact | Minimal |
| FPGA-Based Emulators | Firesim | ≈ 10 MIPS | 2-6 hours | Cycle-exact | $10k+ |
| ASIC-Based Emulators | Palladium, Veloce | ≈ 0.5-10 MIPS | <1 hour | Cycle-exact | $10M+ |
- There is no simulation technique that meets all our criteria:
- High throughput: same order as interpreted ISA simulators
- Low latency: startup time ≈ RTL simulator compilation
- Accurate: small IPC errors, usable for evaluating optimizations
- Low cost: usable by academics
Accuracy of Microarchitectural Simulators
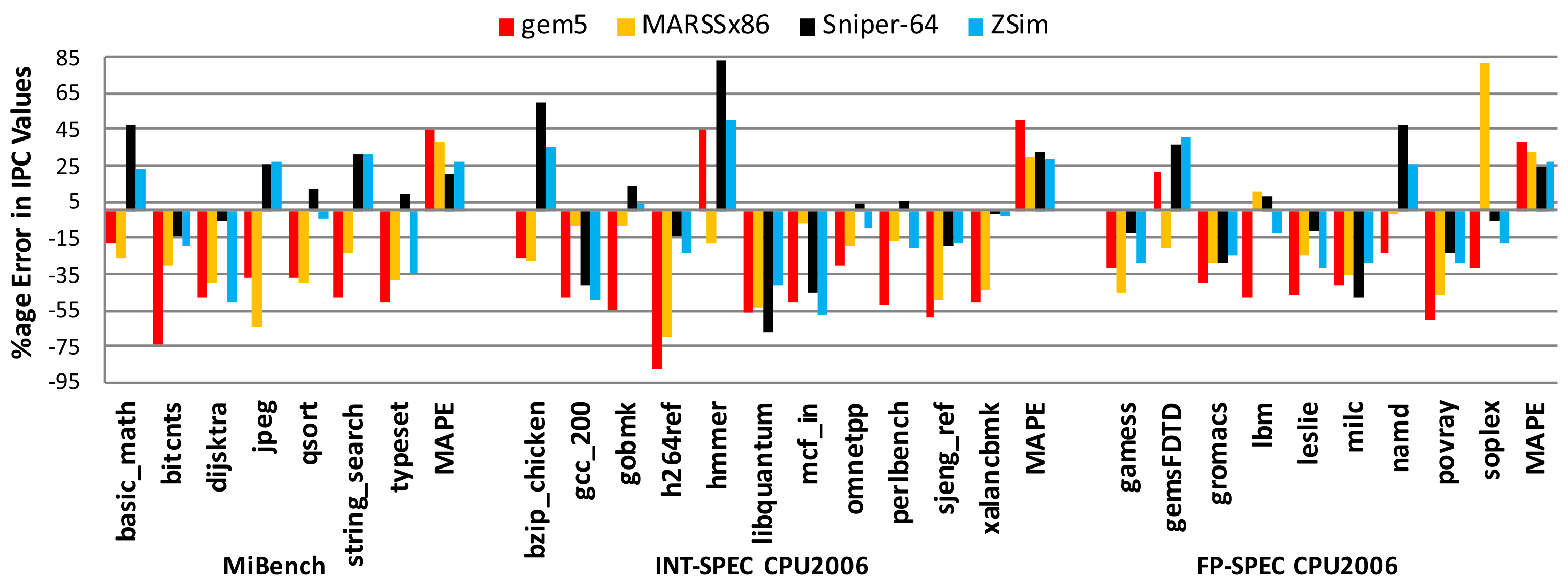
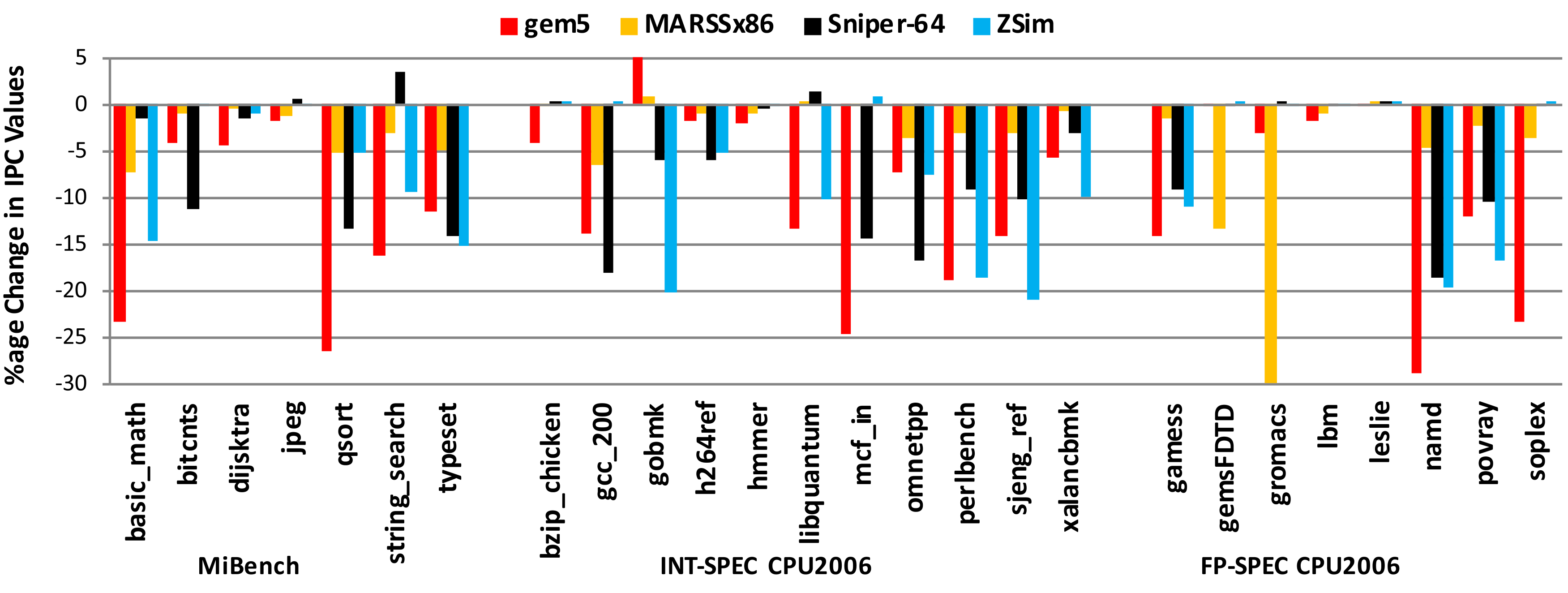
Trends aren't enough[2]. Note the sensitivity differences - gradients are critical!
uArch simulators are not accurate enough for microarchitectural evaluation.
[2]: Nowatzki, T., Menon, J., Ho, C.H. and Sankaralingam, K., 2015. Architectural simulators considered harmful. Micro.
What are we trying to solve?
We want a tool to evaluate (RTL-level) microarchitectural changes on real workloads at high fidelity
Why is this worth solving?
Enabling The "RTL-First" Methodology
- "Design-first", don't model!
- Build the whole system and evaluate it directly
- Iterate at the system-level
- Single source of truth
- Maintaining models that need to match the RTL creates more problems than it solves
- Iterate on the design directly
- This methodology works
- The "design-first" approach has built robust, high-performance open source RISC-V IP (rocket-chip, BOOM, Hwacha, Chipyard, Constellation) with small teams of grad students
- This methodology demands new tools
- FireSim: FPGA-accelerated deterministic RTL simulation
- But, FireSim isn't suitable for rapid iteration
Why RTL-Level Sampled Simulation?
- Eliminate modeling errors
- No need to correlate performance model and RTL
- Let the RTL serve as the source of truth
- Can produce RTL-level collateral
- Leverage for applications in verification and power modeling
What are we trying to solve?
We want a tool to evaluate (RTL-level) microarchitectural changes on real workloads at high fidelity
Why is this worth solving?
Build a critical and novel tool to enable the "design-first" methodology and leverage our RTL designs
Background
Sampled Simulation
Instead of running the entire program in uArch simulation, run the entire program in functional simulation and only run samples in uArch simulation
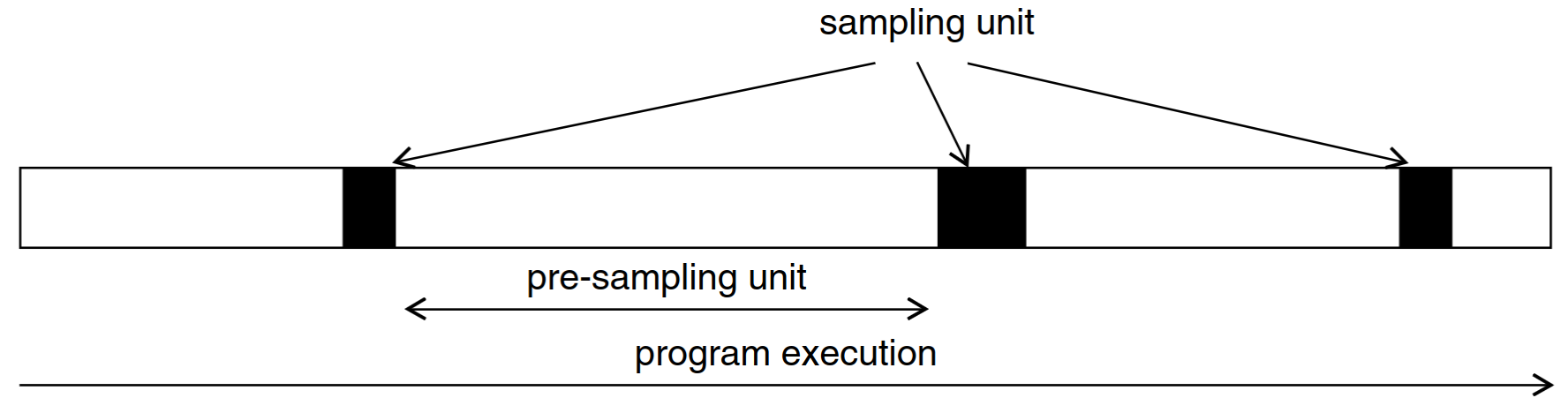
The full workload is represented by a selection of sampling units.
- How should sampling units be selected?
- How can we accurately estimate the performance of a sampling unit?
- How can we estimate errors when extrapolating from sampling units?
Existing Sampling Techniques
SimPoint

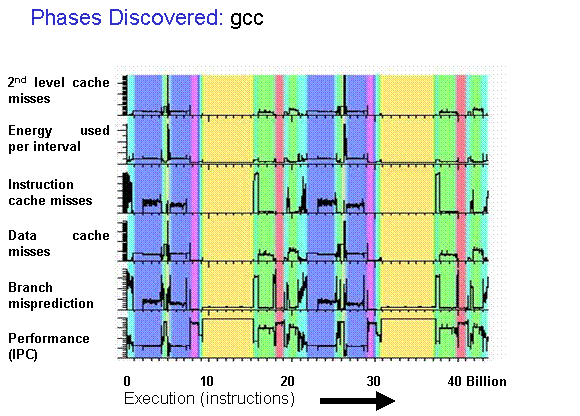
- Workloads can be split into phases that exhibit similar μArch behavior
- SimPoint-style representative sampling
- Compute an embedding for each program interval (e.g. blocks of 100M instructions)
- Cluster interval embeddings using k-means
- Choose representative intervals from each cluster as sampling units
SMARTS

- If we sample from a population, we can estimate the population mean
- SMARTS-style random sampling
- Pick a large number of samples to take before program execution
- If the sample variance is too high after simulation, then collect more sampling units
- Use CLT to derive a confidence bound for the aggregate performance metric
Our proposal: Combine SimPoint-style representative sampling with SMARTS-style small intervals
Functional Warmup
The state from a sampling unit checkpoint is only architectural state. The microarchitectural state of the uArch simulator starts at the reset state!

- We need to seed long-lived uArch state at the beginning of each sampling unit
- This process is called functional warmup
TidalSim Implementation
Overview of the TidalSim Flow
Implementation Details For TidalSim
- Basic block identification
- BB identification from spike commit log or from static ELF analysis
- Basic block embedding of intervals
- Clustering and checkpointing
- k-means, PCA-based n-clusters
- spike-based checkpoints
- RTL simulation and performance metric extraction
- Custom force-based RTL state injection, out-of-band IPC measurement
- Extrapolation
- Estimate IPC of each interval based on its embedding and distances to RTL-simulated intervals
Overall Functional Warmup Flow
- uarch-agnostic cache checkpoints as memory timestamp record (MTR) checkpoints
- MTR checkpoints → cache state with cache parameters and DRAM contents
- RTL simulation harness injects cache state into L1d tag+data arrays via 2d reg forcing
Memory Timestamp Record
- Construct MTR table from a memory trace, save MTR tables at checkpoint times
- Given a cache with n sets, group block addresses by set index
- Given a cache with k ways, pick the k most recently accessed addresses from each set
- Knowing every resident cache line, fetch the data from the DRAM dump
DEMO!
- Sampled RTL simulation with spike, L1d warmup models, and VCS
- Embench workload
Results
IPC Trace Reconstruction - wikisort
wikisort benchmark from embench, $N = 10000$, $C = 18$, $n_{\text{detailed}} = 2000$
IPC Trace Reconstruction - huffbench
huffbench benchmark from embench, $N = 10000$, $C = 18$, $n_{\text{detailed}} = 2000$
WIP: Detailed Error Analysis
Questions We Want to Answer
- How good would RTL sampled simulation be if we had perfect warmup?
- What is the breakdown of sampling vs detailed/functional warmup related errors?
- Can we predict the error of sampled simulation before running it?
Let's build a methodology for answering these questions
Eliminating Sampling Errors
- Let's inject only arch state into RTL sim and simulate each interval
- This is the worst case / maximum error for that interval
- We can measure the error reduction of each thing we do (functional / detailed warmup)
- The remaining error can be attributed to sampling
Evaluating Detailed Warmup Errors
- Let's begin by seeing the impact of only detailed warmup
- We can play with the offset of injection to evaluate its role too
Evaluating Functional Warmup Errors
- Add functional warmup (using a model or a perfect oracle) to the mix
WIP: This methodology enables error analysis of sampling and warmup.
Backup Slides
Evaluation - Detailed Warmup Alone
For a given workload interval and a interval length $N$ (e.g. $N = 10000$) and without functional warmup, we can compute this table. (each cell is IPC error wrt the full RTL simulation)
| Detailed warmup instructions ($ n_{\text{warmup}} $) | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 100 | 500 | 1000 | 2000 | 5000 | ||
| Detailed warmup offset ($ n_{\text{offset}} $) | 0 | Worst case | Offset error ↑ Warmup error ↓ |
Offset error 2↑ Warmup error 2↓ |
Offset error 3↑ Warmup error 3↓ |
Offset error 4↑ Warmup error 4↓ |
Maximum offset error |
| -100 | Invalid | No offset error | '' | '' | '' | '' | |
| -500 | No offset error | '' | '' | '' | |||
| -1000 | No offset error | '' | '' | ||||
| -2000 | No offset error | '' | |||||
| -5000 | No offset error, best case | ||||||
Detailed Warmup Error Model
Given the data in the table for every interval and for different interval lengths $N$, fit the following model:
- Logistic term to model error reduction from warmup
- Linear term to model error reduction from offset elimination
- Linear term to model relationship of interval length to IPC error
- There might also be a term that mixes $n_{\text{warmup}}$ and $n_{\text{offset}}$ (TBD)
Extending the Error Model
- Consider building more tables with different functional warmup types (L1i, L1d, L2, BP, combinations) and fidelity (perfect vs model)
- Still an open question: how can we mix the functional warmup type/fidelity into the error model?
- Given a particular sampled simulation configuration ($N$, $n_{\text{warmup}}$, $n_{\text{offset}}$, functional warmup type + fidelity) for a given workload
- The remaining error from the table cell is attributable to inaccurate warmup (functional + detailed)
- Any additional error seen in actual sampled simulation is attributable to embedding
Conclusion
- We need fast, low-startup-latency RTL-level simulation
- We propose a simulation methodology based on sampled RTL simulation
- Small intervals + functional warmup with RTL simulation
- Everything is open source
- TidalSim (github.com/euphoric-hardware/tidalsim) Forks of spike, chipyard, testchipip + top-level runner